ONE TO NINE by Andrew Hodges

Notes, links, updates and answers for Chapter Four.

Answers to Problems

 Page 107:

If £1000 increases by 41.4% it becomes £1414. If it increases by 41.4% again it becomes £1414 × 1.414 = £1999.40.

Page 109:

The 'how many days' question is exactly what the logarithm answers. What power of 2 makes a million? From the approximation 1000 ≈ 1024, it is about 20.

The logarithm of 4 to base 2 is 2. The logarithm of 2 to base 4 is 1/2, which is equivalent to saying the 2 is the square root of 4.

Again we use 1000 ≈ 1024, i.e. 103 ≈ 210. Take the tenth root of each side, and this shows 100.3 ≈ 2.

Page 109: Billy Bragg didn't see the point of logarithms.

Page 116: The method for finding square roots that used to be taught in schools is explained here. It is further discussed on this page.

Answers to Problems

 Page 118:

Start with 577/408 and apply the jumping-ahead formula twice to find first 665857/470832, then 88673108897/627013566048.

To see the accuracy, suppose that m/n is one of these fractions, so that m2 − 2 n2 = ± 1.
Then (m/n)2 = 2 ± 1/n2. When n = 627013566048 this differs from 2 by less than 10− 23, which also means that m/n differs from √2 by less than 10− 23.

To see that every pair with m2 − 2 n2 = ± 1 is in this sequence, use an argument by contradiction. Suppose there is some such pair, then there must be a least one. But now use the generating method in reverse.
Let p = 2n − m, q = m − n. Then p2 − 2 q2 = (2n− m)2 - 2 (m − n)2 = − m2 + 2n2 = ± 1. So the pair (p,q) is a smaller pair satisfying the property, but it cannot be in the sequence because if it were then (m, n) would be. This is a contradiction, so the sequence contains all such pairs.

Answers to Problems

 Page 120:

Take a pair (m/n) in the sequence for √2, where n is even, so m2 − 2 n2 = 1.
Then ((m − 1)/2 + n, (m + 1)/2 + n, m + n) is a Pythagorean triple with two sides differing by 1.

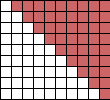The picture immediately gives the explanation of how to add the numbers from 1 to 9. Two such triangles make a rectangle of 9 × 10 squares, and half of this is 45. To add the numbers from 1 to 100, take half of 100 × 101, which is 5050.

Page 121:

If the triangular number s(s+1)/2 is square, then either s+1 is square and s/2 is square, or s is square and (s+1)/2 is square.
These are equivalent to taking s = m2 − 1 when m2 − 1 = 2n2, and s= m2 when m2+ 1 = 2n2.
We know the solutions to these equations from the approximations to √2. Thus the sequence of possible numbers s runs:

12, 32 − 1, 72, 172 − 1, 412, 992 − 1... where the numbers 1, 3, 7, 17, 41, 99... come from the approximations to √2.

These give the triangular numbers 1, 36, 1225, 41616, 1413721, 48024900...

Back to index page | Chapter 5